Uno de los fundadores de la trigonometría; “Regiomontanus”.

El 6 de julio de 1476, fallecía el astrónomo y matemático alemán Johann Müller Königsberg y el conocido popularmente como «Regiomontano» o “Regiomontanus” (Königsberg en Bayern (Franconia), 6 de junio de 1436 – Roma, 6 de julio de 1476).

 

El apodo de»Regiomontano» o “Regiomontanus”, es debido a su ciudad de nacimiento, Königsberg que en su traducción latina significa Montaña real o Montaña Regia. Otro Regiomontano destacado es Immanuel Kant. Curiosamente los habitantes de Monterrey en Mexico, reciben también ese apodo.

Regiomontano a la edad de once años se matriculó en la Universidad de Leipzig para estudiardialéctica, continuando los estudios universitarios desde 1447 hasta 1450. Ese mismo año ingresó en la Universidad de Viena donde permanecería hasta 1957.

En noviembre de 1457, la Facultad de Arte de la Universidad de Viena le eligió para colaborar con los trabajos de su antiguo profesor Peuerbach.

En el terreno de la observación astronómica, los dos astrónomos hicieron observaciones de Marte y lograron predecir correctamente su posición. Regiomontanus daba cursos en la universidad sobre: perspectiva, geometría de Euclides y de literatura (Bucólicas de Virgilio). Durante este periodo trabajó en matemáticas, astronomía y construyó instrumentos tales como astrolabios.

En 1461 viaja a Roma para alistarse a las órdenes del Cardenal Basilio Besarión para poder realizar diseños sobre astrolabios y relojes de sol.

En 1471 viaja a Núremberg y allí establece un observatorio con el patrocinio de Bernard Walther, en el que realiza actividades de investigación, cálculo y observación de fenómenos astronómicos. En enero de 1472 hizo observaciones de un cometa y lo describió (270 años después fue igualmente descrito porHalley y se convirtió en el cometa de Halley).

Entre los años 1471 y 1472 actuó como un impresor en su propia casa de Núremberg. Probablemente fuera el primer impresor de literatura científica. Su primera obra como impresor fue el libro de su exprofesor Peuerbach sobre la teoría de los movimientos planetarios, siendo la siguiente impresión en el año 1474, en el que edita su propio «Kalendarium» y su «Ephemerides».

La obra escrita de Regiomontano se puede englobar en tratados de matemática, centrados en lo que hoy se denomina trigonometría (se le considera un fundador de esta parte de la matemática) y tratados sobre astronomía. Por otra parte describe e inventa varios instrumentos útiles para la observación y la medida del tiempo (relojes solares). Todo este apartado lo divulga en una especie de panfletos impresos que fueron muy leídos durante su época.

La trigonometría es una rama de la matemática, cuyo significado etimológico es ‘la medición de los triángulos’. Deriva de los términos griegos τριγωνοϛ trigōnos ‘triángulo’ y μετρον metron ‘medida’

Durante muchos siglos, la trigonometría de Ptolomeo fue la introducción básica para los astrónomos. Su libro de Astronomía, el Almagesto, también tenía una tabla de cuerdas junto con la explicación de su método para compilarla, y a lo largo del libro mostraba ejemplos de cómo utilizar dicha tabla para calcular los elementos desconocidos de un triángulo a partir de los conocidos.
El teorema de Menelao utilizado para resolver triángulos esféricos fue autoría de Ptolomeo.

Al mismo tiempo, los astrónomos de la India habían desarrollado también un sistema trigonométrico basado en la función seno en vez de cuerdas como los griegos. Esta función seno, era la longitud del lado opuesto a un ángulo en un triángulo rectángulo de hipotenusa dada. Los matemáticos hindúes utilizaron diversos valores para ésta en sus tablas.

A finales del siglo VIII los astrónomos árabes trabajaron con la función seno y a finales del siglo X ya habían completado la función seno y las otras cinco funciones. También descubrieron y demostraron teoremas fundamentales de la trigonometría, tanto para triángulos planos como esféricos. Los matemáticos sugirieron el uso del valor r = 1 en vez de r = 60, y esto dio lugar a los valores modernos de las funciones trigonométricas.

El Occidente latino se familiarizó con la trigonometría árabe a través de traducciones de libros de astronomía arábigos, que comenzaron a aparecer en el siglo XII. El primer trabajo importante en esta materia en Europa fue escrito precisamente por Regiomontanus.

De triangulis, la obra tal vez más importante de Regiomontano, se compone de cinco libros, en el primero da las definiciones básicas: cantidad, ratio, igualdad, círculos, arcos, cuerdas y la función seno. Proporciona algunos axiomas que serán el sustento de los 56 teoremas que enunciará.

En el segundo de los libros establece la Ley del seno (en trigonometría, el teorema de los senos, también conocido como ley de los senos es una relación de proporcionalidad entre las longitudes de los lados de un triángulo y los senos de sus respectivos ángulos opuestos) y la emplea en la resolución de algunos problemas con triángulos.

Determina el área de un triángulo mediante el conocimiento de dos lados y el ángulo que los sustenta. Los libros III, IV y V tratan de trigonometría esférica centrando el tema para las posteriores obras de astronomía.

La trigonometría esférica es la parte de la geometría esférica que estudia los polígonos que se forman sobre la superficie de la esfera, en especial, los triángulos. La resolución de triángulos esféricos tiene especial relevancia en astronomía náutica y navegación para determinar la posición de un buque en alta mar mediante la observación de los astros.

En su estancia en Hungría, Regiomontanus calcula dos tablas de senos. La primera la realiza en 1467 y emplea una división sexagesimal de los ángulos, la otra calcula los senos de un ángulo empleando una división decimal.

En el terreno de la astronomía, Regiomontanus también publicó el trabajo «Epitome in Almagestum» (publicado póstumamente en 1498). Se trata de un libro en el que expone el sistema de Ptolomeo.

La teoría de la relatividad general; Einstein.

El 20 de marzo de 1916, la prestigiosas revista científica alemana Annalen der Physik recibe el artículo de Albert Einstein, “Die Grundlagen der allgemeinen Relativitästheorie.” (Los fundamentos de la teoría general de la relatividad).

 

Sería publicado con la siguiente referencia Annalen der Physik 1916, 354 (7), 769-822.

 

En el artículo, Einstein reformulaba por completo el concepto de gravedad. Una de las consecuencias fue el surgimiento del estudio científico del origen y la evolución del Universo por la rama de la física denominada cosmología.

 

En 1905 Albert Einstein ya había revolucionado al mundo al redactar lo que ahora conocemos como teoría de la relatividad especial. Esta teoría se basaba en el Principio de relatividad y en la constancia de la velocidad de la luz en cualquier sistema de referencia inercial. Einstein dedujo las ecuaciones de Lorentz. También reescribió las relaciones del momento y de la energía cinética para que éstas también se mantuvieran invariantes.

La teoría surgía de la observación de que la velocidad de la luz en el vacío es igual en todos los sistemas de referencia inerciales y de obtener todas las consecuencias del principio de relatividad de Galileo, según el cual cualquier experimento realizado, en un sistema de referencia inercial, se desarrollará de manera idéntica en cualquier otro sistema inercial.

 

 Entre 1914 y 1916, Einstein, centró sus esfuerzos en el perfeccionamiento de la teoría general de la relatividad, basada en el postulado de que la gravedad no es una fuerza sino un campo creado por la presencia de una masa en el continuum espacio-tiempo.

 

El nombre de la teoría general se debe a que generaliza la teoría especial de la relatividad. Los principios fundamentales introducidos en esta generalización son el Principio de equivalencia, que describe la aceleración y la gravedad como aspectos distintos de la misma realidad, la noción de la curvatura del espacio-tiempo y el principio de covariancia generalizado.

 

La intuición básica de Einstein fue postular que en un punto concreto no se puede distinguir experimentalmente entre un cuerpo acelerado uniformemente y un campo gravitatorio uniforme. 

 

Poco después de la formulación de la teoría de la relatividad especial en 1905, Albert Einstein comenzó a pensar cómo describir los fenómenos gravitatorios con ayuda de la nueva mecánica.

 

En 1907 se embarcó en la búsqueda de una nueva teoría relativista de la gravedad que duraría ocho años. Después de numerosos desvíos y falsos comienzos, su trabajo culminó en noviembre de 1915 con la presentación a la Academia Prusiana de las Ciencias de su artículo, que contenía las que hoy son conocidas como “Ecuaciones de Campo de Einstein”. Estas ecuaciones forman el núcleo de la teoría y especifican cómo la densidad local de materia y energía determina la geometría del espacio-tiempo.

 

En 1917, Einstein aplicó su teoría al universo en su conjunto, iniciando el campo de la cosmología relativista. En línea con el pensamiento contemporáneo, en el que se suponía que el universo era estático, agregó a sus ecuaciones una constante cosmológica para reproducir esa “observación”.

 

En 1929, sin embargo, el trabajo de Hubble y otros demostraron que nuestro universo se está expandiendo. Esto es fácilmente descrito por las soluciones encontradas por Friedmann en 1922 para la expansión cosmológica, que no requieren de una constante cosmológica. Lemaître utilizó estas soluciones para formular la primera versión de los modelos del Big Bang, en la que nuestro universo ha evolucionado desde un estado anterior extremadamente caliente y denso. Einstein declaró más tarde que agregar esa constante cosmológica a sus ecuaciones fue el mayor error de su vida.

 

El 29 de mayo de 1919, la teoría de la relatividad general de Einstein es comprobada (y posteriormente confirmada) por el astrónomo inglés Arthur Stanley Eddington (28 de diciembre de 1882 en Kendal-22 de noviembre de 1944 en Cambridge) mediante la observación de un eclipse solar total en la isla Príncipe y por Andrew Crommelin en Sobral, Ceará (Brasil). Durante el eclipse fotografió las estrellas que aparecían alrededor del Sol. Según la Teoría de la Relatividad General, las estrellas que deberían aparecer cerca del Sol deberían estar un poco desplazadas, porque su luz es curvada por el campo gravitatorio solar. Este efecto sólo puede observarse durante un eclipse, ya que si no el brillo del Sol hace las estrellas invisibles al ojo humano.

 

Las observaciones de Eddington confirmaron la teoría de Einstein, y fueron tomadas en su época como la prueba de la validez de la relatividad general frente a la en parte obsoleta mecánica newtoniana.

 

Sin embargo, la teoría de la relatividad general fue especialmente valorada por la física teórica y la astrofísica desarrolladas aproximadamente entre 1960 y 1975, ahora conocido como la edad de oro de la relatividad general. Los físicos empezaron a comprender el concepto de agujero negro, y a identificar la manifestación de objetos astrofísicos como los cuásares. Cada vez más precisas, las pruebas del sistema solar confirmaron el poder predictivo de la teoría, y la cosmología relativista, también se volvió susceptible a encaminar pruebas observacionales.

 

La teoría de la relatividad general ha sido confirmada en numerosas formas desde su aparición. Por ejemplo, la teoría predice que la línea del universo de un rayo de luz se curva en las proximidades de un objeto masivo como el Sol. La primera comprobación empírica de la teoría de la relatividad fue a este respecto.

 

Durante los eclipses de 1919 y 1922 se organizaron expediciones científicas para realizar esas observaciones. Después se compararon las posiciones aparentes de las estrellas con sus posiciones aparentes algunos meses más tarde, cuando aparecían de noche, lejos del Sol.

 

Einstein predijo un desplazamiento aparente de la posición de 1,745 segundos de arco para una estrella situada justo en el borde del Sol, y desplazamientos cada vez menores de las estrellas más distantes.

 

Se demostró que sus cálculos sobre la curvatura de la luz en presencia de un campo gravitatorio eran exactos. En los últimos años se han llevado a cabo mediciones semejantes de la desviación de ondas de radio procedentes de quásares distantes, utilizando interferómetros de radio. Las medidas arrojaron unos resultados que coincidían con una precisión del 1% con los valores predichos por la relatividad general.

 

Otra confirmación de la relatividad general está relacionada con el perihelio del planeta Mercurio. Hacía años que se sabía que el perihelio (el punto en que Mercurio se encuentra más próximo al Sol) gira en torno al Sol una vez cada tres millones de años, y ese movimiento no podía explicarse totalmente con las teorías clásicas. En cambio, la teoría de la relatividad sí predice todos los aspectos del movimiento, y las medidas con radar efectuadas recientemente han confirmado la coincidencia de los datos reales con la teoría con una precisión de un 0,5%.

 

Se han realizado otras muchas comprobaciones de la teoría, y hasta ahora todas parecen confirmarla. Prácticamente con la más reciente prueba del satélite Gravity Probe B, se podría considerar a la teoría como una Ley.

Adiós al “gigante”de «gigantes»; Newton.

El 20 de marzo de 1727, fallecía el físico, filósofo, teólogo, inventor, alquimista y matemático inglés Isaac Newton (Woolsthorpe, Lincolnshire; 25 de diciembre de 1642 jul./ 4 de enero de 1643 greg.-Kensington, Londres; 20 de marzo jul./ 31 de marzo de 1727 greg.), una de las mentes mas brillantes de todos los tiempos.

El físico y matemático Joseph Louis Lagrange (1736-1813), dijo que “Newton fue el más grande genio que ha existido y también el más afortunado dado que sólo se puede encontrar una vez un sistema que rija el mundo”.

¿Qué se puede decir de Newton que no se hubiese dicho ya?. Nada. Posiblemente sea una de las personas más estudiadas de todos los tiempos. No es para menos…Un buen resumen de la vida y obra de  Newton sería simplemente decir, cambió la Historia.

Asombra pensar, que un sólo hombre realizase tantas y tan magníficas contribuciones a la Ciencia.

Se ha hablado de su mal genio (sus enfrentamientos con Leibiniz , Huygens y Hooke, son legendarios). Se ha rumoreado que se aprovechaba del trabajo de otros, de su enorme ego y de su inmenso rencor. Pero lo que es incuestionable, que aún a día de hoy, en el siglo XXI, su figura es imponente.

Cuando el 5 de julio de 1687, Isaac Newton publica Philosophiæ naturalis principia mathematica (Principios matemáticos de la filosofía natural) el mundo y nuestro conocimiento del mismo, simplemente cambió. Se trataba de el libro científico mas importante de todos los tiempos. Y nadie, todavía, ha conseguido cuestionar semejante honor. Newton fue el primero en demostrar que las leyes naturales que gobiernan el movimiento en la Tierra y las que gobiernan el movimiento de los cuerpos celestes son las mismas, casi nada.

Newton comenzó sus estudios en la King’s School de Grantham.

En 1661 ingresó con dieciocho años en la Universidad de Cambridge . Se graduó en el Trinity College en 1665 con mas pena que gloria. No fue un estudiante modélico, ni mucho menos. No asistía de forma regular a clases, prefiriendo la formación autodidácta. Su ego parecía empezar a manifestarse.

A mediados del verano de 1665, la Gran Peste apareció en Londres. En otoño se cerró la Universidad de Cambridge y todos los estudiantes fueron enviados a sus casas.

Newton comentaría con posterioridad que, precisamente, sus años de “exilio” universitario, los comprendidos entre 1665 y 1666 serían los más fructiferos de su carrera, lo que nos da una pequeña idea de su gran espiritu autodidácta. Así escribiría:

“A comienzos de 1665 encontré la… regla para reducir cualquier dignidad
(poder) de los binomios a serie. El mismo año en 1 de mayo descubrí el método de las tangentes… y en noviembre el método directo de las fluxiones (es decir, los elementos de lo que ahora se llama cálculo diferencial) y al año siguiente, en enero, la teoría de los colores, y en el siguiente el método inverso de las fluxiones (es decir, el cálculo integral) y en el mismo año comencé a pensar en la gravedad extendiéndola a la órbita de la Luna… y…comparé la fuerza requerida para mantener la Luna en su órbita con la fuerza de la gravedad en la superficie de la Tierra”.

Tras numerosas  vicisitudes, en octubre de 1667 Newton fue elegido miembro becario del Trinity College. De 1667 a 1669 emprendió investigaciones sobre óptica. En 1669 sucedería al teólogo y matemático inglés Isaac Barrow Barrow (Londres, octubre, 1630 – id., 4 de mayo, 1677) en la cátedra lucasiana en la que se mantendría hasta 1696.

El 5 de julio de 1687, Isaac Newton publica Philosophiæ naturalis principia mathematica (Principios matemáticos de la filosofía natural). El libro científico mas importante de todos los tiempos, donde describe la ley de la gravitación universal y estableció las bases de la mecánica clásica mediante las leyes que llevan su nombre.

El libro que se publicaría a instancias de su amigo Edmond Halley, recoge sus descubrimientos en mecánica y cálculo matemático. Esta obra marcó un punto de inflexión en la historia de la ciencia y es considerada, por muchos, como la obra científica más importante de la Historia.

Su publicación se había demorado enormemente dado el temor de Newton a que otros intentaran apropiarse de sus descubrimientos. Sin embargo Edmond Halley presionó a Newton hasta que publicara, Newton se lo agradece en las primeras páginas del libro. Los tres libros de esta obra contienen los fundamentos de la física y la astronomía escritos en el lenguaje de la geometría pura. El Libro I contiene el método de las “primeras y últimas razones” y, bajo la forma de notas o escollos, se encuentra como anexo del Libro III la teoría de las fluxiones.

Newton trata el programa de la llamada interpretación mecanicista de los fenómenos físicos, un punto de vista que ha dominado la física hasta principios de este siglo y sólo fue corregida con la aparición de la teoría de la relatividad y de la mecánica cuántica.

Llegó a desarrollar  el tratamiento matemático de los fenómenos mecánicos de forma tan  precisa que pueden ser empleados sin alteración en cualquier libro moderno de mecánica clásica.

En el campo de la mecánica recopiló en su obra los hallazgos de Galileo y enunció sus tres famosas leyes del movimiento.

La parte de axiomas o leyes del movimiento comienza indicándonos las famosas tres leyes de Newton.

Entre otras muchas cosas, Newton explicaba el fenómeno de las mareas como debidas a la desigual fuerza gravitatoria ejercida por el Sol sobre los hemisferios terrestres al girar hacia él y lejos de él.

Entre 1670 y 1672, Newton,  trabajó intensamente en problemas relacionados con la óptica y la naturaleza de la luz.

El 8 de de febrero de 1672, Isaac Newton, lee su primer escrito relativo a la óptica delante de la Royal Society en Londres; “Nueva teoría sobre la luz y los colores ” Newton demostró que cualquier telescopio refractor sufriría de un tipo de aberración conocida en la actualidad como aberración cromática, que consiste en la dispersión de la luz en diferentes colores al atravesar una lente. Para evitar este problema había inventado un telescopio reflector.  El telescopio de Newton constaba de un espejo primario cóncavo y un espejo secundario de plano diagonal. Eligió una aleación (espéculo de metal) de estaño y cobre como los materiales más adecuados para su espejo objetivo. El primer telescopio de este tipo estaba finalizado a finales de 1968.

Newton demostró, además,  que la luz blanca estaba formada por una banda de colores (rojo, naranja, amarillo, verde, cian, azul y violeta) que podían separarse por medio de un prisma.  Hizo pasar un haz de luz solar a través de un prisma de cristal de forma triangular, y comprobó que el haz originaba una banda constituida por luz roja, naranja, amarilla, verde, azul y violeta, y que cada color pasaba al próximo mediante una transición suave.

Lo que Newton demostró fue que la luz solar, o “luz blanca”, era realmente una mezcla de muchas radiaciones específicas (que hoy reconocemos como formas ondulatorias, de diversa longitud de onda), las cuales excitan el ojo humano, determinando la percepción de los citados colores. El prisma los separa, debido a que, al pasar del aire al cristal y de éste a aquél, la luz es desviada en su trayectoria o “refractada”, y cada longitud de onda experimenta cierto grado de refracción, la cual es mayor cuanto más corta es la longitud de onda

En base a los experimentos realizados sobre la naturaleza de la luz Newton formuló su teoría general. Para Newton la luz estaba formada por corpúsculos y se propagaba en línea recta y no por medio de ondas. A raíz de estas conclusiones comenzaría su disputa con Hooke  y Huygens, firmes defensores de la la naturaleza ondulatoria de la luz, y  que se prolongaría durante años. Ahora sabemos que la luz tiene una naturaleza dual: es onda y corpúsculo al mismo tiempo. Pero para esta conclusión  haría falta el surgimiento de un nuevo tipo de física, la mecánica cuántica, hecho que no se produciría hasta el siglo XX.

En 1704, Newton escribiría su obra más importante sobre óptica, Opticks, “Un tratado de las reflexiones, refracciones, inflexiones y colores de la luz”, en la que exponía sus teorías anteriores y la naturaleza corpuscular de la luz, así como un estudio detallado sobre fenómenos como la refracción, la reflexión y la dispersión de la luz.

En la parte de definiciones comienza con rayo de luz, refrangibilidad y reflexibilidad, ángulo de incidencia, ángulo de reflexión, luz simple, senos de incidencia, reflexión y refracción. En la parte de Axiomas describe como se comportan los rayos de luz y describe las propiedades de los ángulos ya mencionados.

También expone lo que se conoce como la ley de Snell para distintos casos, como son espejo plano, espejo esférico, superficie plana, superficie, esférica, lentes y prismas. Además introduce una sencilla explicación del funcionamiento del ojo humano.

En  1701 Newton s enunció definitivamente a su cátedra y a su condición de investigador del Trinity College. En 1703, tras la muerte de Hooke y, Newton fue elegido presidente de la Royal Society, cargo que conservó hasta su muerte. En 1705 se le otorgó el título de sir.

El “gigante” finalmente moriría la noche del 20 de marzo de 1727 (calendario gregoriano).

Fue enterrado en la abadía de Westminster. Un honor resevado a los grandes hombres de Inglaterra.

Como colofón, destacar que Isaac Newton en una carta remitida el 15 de febrero de 1676 (el 5 de febrero de 1675 en el calendario juliano de la época) a Robert Hooke, escribió: “Si he visto más lejos es porque estoy sentado sobre los hombros de gigantes” (nos esse quasi nanos, gigantium humeris incidentes). La cita pertenecía en realidad a Bernardo de Chartres, pero ha quedado ligada para siempre a Newton.

El día de π.

El 14 de marzo, anualmente, se conmemora el día de π. Se realiza ese día por el formato usado en los Estados Unidos, para escribir el 14 de marzo (3/14)

Fue una propuesta del físico Larry Shaw para popularizar la ciencia y que se ha hecho mundialmente famosa con numerosos actos.

En 2009 una resolución favorable de la Cámara de Representantes de los Estados Unidos, declaraba al 14 de marzo como día nacional de π.

El día Pi «perfecto», sólo se produce cada 100 años. Ocurrió el 14 de marzo del año 2015 (3/14/15) que coincidía con los primeros números de la constate π (3’141592653).

Fue un acontecimiento con una una enorme repercusión a nivel mundial, especialmente  en las redes sociales.

Lo cierto es que pi es una constante matemática muy atractiva (tal vez la más atractiva junto con e) para el público en general.

π (pi) es la relación entre la longitud de una circunferencia y su diámetro, en geometría euclidiana. Pi (π) tiene un valor aproximado de 3,14159265358979… Desde tiempos inmemoriales se ha tratado de obtener su valor exacto. En el papiro Rhind del escriba egipcio Ahmes en el año1800 a. C., ya aparece un intento de obtener su valor. Hoy en día sólo sabemos que cuenta con billones de dígitos que siguen aumentando.

La notación con la letra griega π proviene de la inicial de las palabras de origen griego περιφέρεια ‘periferia’ y περίμετρον ‘perímetro’ de un círculo- El rpiemro en emplear esta notación nor William Oughtred (1574-1660) aunque realmente su uso fue popularizado por el ”gigante” matemático Leonhard Euler (Basilea, Suiza, 15 de abril de1707 – San Petersburgo, Rusia, 18 de septiembre de 1783), en su obra de 1748 “Introductio in analysin infinitorum“ (Introducción al cálculo infinitesimal).

Como anécdota histórica, ell 5 de febrero 1897, en el estado estadounidense de Indiana, se propuso por Ley otorgar un valor fijo y único a pi: 3,2. El proyecto de ley de Indiana sobre π (Pi) (en inglés Indiana Pi Bill).

En la Asamblea General de Indiana, se tramitó el proyecto de Ley No.246. “Un proyecto de ley que presenta una nueva verdad matemática y que es ofrecido como una contribución a la educación que solo podrá ser utilizado por el Estado de Indiana en forma gratuita sin necesidad de pagar ningún tipo de royalties, siempre y cuando sea aceptado y adoptado en forma oficial por la legislatura en 1897”.

Se convertiría en una de las propuestas más absurdas de legislar sobre la Ciencia en la Historia.

La propuesta fue planteada por el representante de la Asamblea General Taylor en nombre de un aficionado a las matemáticas, el Dr. Edwin J. Goodwin, un médico del Estado, que había planteado lo siguiente:

“La relación entre el diámetro y la circunferencia [PI] es de cinco cuartas partes a cuatro. Es decir (4 dividido por 5/4 = 16/5 = 3,2 exactamente”.

El proyecto fue aprobado por la Asamblea General de Indiana por unanimidad (67 votos favorables y ninguno contrario…).

Por fortuna, cuando el Proyecto de Ley se estaba tramitando en el Senado (después de obtener el informe favorable del Comité de Educación…) un profesor de la Universidad Perdue de Lafayette, el matemático Clarence A. Waldo Clarence Abiathar Waldo (January 21, 1852 – October 1, 1926), demostró la incoherencia matemática de tal aseveración.

Waldo debió ser muy persuasivo ya que el Proyecto de Ley fue pospuesto el 12 de febrero de 1897 de forma indefinida.

Historias de gigantes (VII). La primera mujer astrónoma; Hipatia de Alejandría.

El 8 de marzo del año 415 es asesinada Hipatia de Alejandría, filósofa, astrónoma y escritora egipcio-romana. Una «gigante» de la historia de la ciencia.

Hipatia o Hypatia (Alejandría, 355 o 370–ibíd., 8 de marzo de 415 o 416) fue una filósofa y maestra neoplatónica griega, natural de Egipto, que destacó en los campos de las matemáticas y la astronomía. Seguidora de Plotino, cultivó los estudios lógicos y las ciencias exactas, llevando una vida ascética.

Educó a una selecta escuela de aristócratas cristianos y paganos que ocuparon altos cargos, entre los que sobresalen el obispo Sinesio de Cirene, que mantuvo una importante correspondencia con ella, Hesiquio de Alejandría y Orestes, prefecto de Egipto en el momento de su muerte.

Hipatia nació en Alejandría, capital de la diócesis romana de Egipto, a mediados del siglo IV, en 370, según algunas referencias, y en 355, al decir de otras. Pero dado que su discípulo Sinesio de Cirene nació en torno a 375, esta última fecha parece la más correcta. Su padre fue Teón de Alejandría, un célebre matemático y astrónomo, muy apreciado por sus contemporáneos, que probablemente debió trabajar y dar clases en la Biblioteca del Serapeo, sucesora de la legendaria Gran Biblioteca ptolemaica. Hipatia, por su parte, se educó en un ambiente académico y culto, dominado por la escuela neoplatónica alejandrina, y aprendió matemáticas y astronomía de su padre, quien además le transmitió su pasión por la búsqueda de lo desconocido.

Hipatia es la primera mujer astrónoma de la que se tiene conocimiento razonablemente seguro y detallado. Escribió sobre geometría, álgebra y astronomía, mejoró el diseño de los primitivos astrolabios, instrumentos para determinar las posiciones de las estrellas sobre la bóveda celeste e inventó un densímetro.

No hay evidencia de que Hipatia haya hecho investigación original en matemáticas, pero su contribución en astronomía fue notable.
Hypatia observó que la obra de Tolomeo daba lugar a numerosas conclusiones matemáticas, de las que su padre no se había dado cuenta. Hypatia calculó los valores matemáticos de los acontecimientos celestes descritos por Tolomeo. Las Tablas o Canon Astronómico serían el resultado de ello.

Otras de sus contribuciones científicas fueron la invención de un buen número de aparatos. En las Cartas de Sinesio, su discípulo preferido, están incluidos sus diseños para varios instrumentos, incluyendo un astrolabio plano, que nos sirve para medir la posición de las estrellas, los planetas y el Sol, y para calcular el tiempo y el signo ascendente del zodíaco. Hypatia no solo sabía utilizar el astrolabio sino que sabía cómo construirlo. Se conservan cartas en las que su discípulo, Sinesio, le pide consejo para la construcción de un astrolabio que servía para medir la altura del Sol y de las estrellas como elemento imprescindible para no perderse en la navegación marítima en un universo geométrico.

Hypatia se interesó por la mecánica y las tecnologías prácticas. También desarrolló un aparato para la destilación del agua, así como un hidroscopio para medir la presencia y el nivel del agua, y un hidrómetro graduado de latón para determinar el peso específico de los líquidos.

Hipatia trabajó junto a su padre en la preparación de textos para los alumnos (entre otros el de los Elementos de Euclides, que reeditó críticamente) y escribió comentarios sobre la Aritmética de Diofanto, el Almagesto de Tolomeo y las Cónicas de Apolonio. Se interesó además por los mecanismos prácticos que usaba para el trabajo en astronomía, elaborando tablas de los movimientos de los cuerpos celestes, aunque se consagró principalmente al estudio y a la enseñanza de las matemáticas.
Durante veinte años se dedicó a enseñar todos estos conocimientos en el Museo de Alejandría e incluso llegó a dirigirlo alrededor del año 400, tras la muerte de su padre Teón.

Ninguna de sus obras se ha conservado, pero se conocen gracias a sus discípulos, como Sinesio de Cirene o Hesiquio de Alejandría:

.- Comentario a la Aritmética en 14 libros de Diofanto de Alejandría. Canon astronómico.
.- Comentario a las Secciones cónicas de Apolonio de Perga.
.- Tablas astronómicas: revisión de las del astrónomo Claudio Tolomeo.
.- Edición del comentario de su padre a Los Elementos de Euclides.

Se dedicó a la enseñanza de la filosofía, centrándose en las obras de Platón y Aristóteles. La casa de Hipatia se convirtió en un lugar de enseñanza donde acudían estudiantes de todas partes del mundo conocido, atraídos por su fama.

Su proceder tolerante, no discriminatorio con sus discípulos, y sus enseñanzas fomentadoras de la racionalidad le fueron creando en la ciudad envidias y odios entre el obispo Cirilo y sus seguidores cristianos.

Las causas de la muerte de Hipatia, sin embargo, distan de ser claras. Su asesinato tuvo motivaciones políticas y según algunos autores religiosas, dentro de la lucha que mantenían el patriarca Cirilo y el prefecto romano Orestes por la hegemonía política en Alejandría.

Empezó a correr entre los cristianos de Alejandría el rumor de que la causante de la discordia entre Cirilo y Orestes era la influyente Hipatia, amiga y consejera de su ex alumno y, presumiblemente, opuesta a los abusos del poder religioso. En plena Cuaresma, un grupo de fanáticos dirigidos por un lector de nombre Pedro se abalanzó sobre la filósofa mientras regresaba en carruaje a su casa, la golpearon y la arrastraron por toda la ciudad hasta llegar al Cesáreo, magno templo edificado por Augusto tras su victoria sobre Marco Antonio y convertido en catedral de Alejandría.

Allí, tras desnudarla, la golpearon con piedras y tejas hasta descuartizarla y sus restos fueron paseados en triunfo por la ciudad hasta llegar a un lugar denominado el Cinareo (por su nombre, se supone que es un crematorio), donde los incineraron.

Una muerte absurda e inexplicablemente cruel para una mujer que dedicó su vida a la enseñanza del conocimiento. Por fortuna, su vida y obra han sido recogidas en numerosos libros y testimonios. Nunca quedará en el olvido.

El asteroide (238) Hypatia (descubierto en 1884) y el cráter lunar Hipatia fueron bautizados en su honor.

A unos 70 km al norte del cráter se halla un sistema de canales de 180 km de longitud llamado Rimae Hypatia, un grado al sur del ecuador lunar, a lo largo del Mare Tranquillitatis.

En octubre de 2013 se encontró un cometa que colapsó con la Tierra hace 28 millones de años en el Desierto de Sahara y se le nombró Hipatia.

El «gigante» incomprendido; Boltzmann.

El 20 de febrero de 1844 , nacía el físico austriaco Ludwig Eduard Boltzmann (Viena, 20 de febrero de 1844 – Duino, Italia, 5 de septiembre de 1906).

Su labor científica estuvo encaminada fundamentalmente a establecer cómo el movimiento de los átomos y su mutua interacción determina las propiedades visibles, macroscópicas, de la materia, tales como presión, viscosidad, conductividad térmica y difusión. Se le considera uno de los “padres” de la mecánica estadística.

Cursó estudios medios en otra ciudad, Linz, y se doctoró en la Universidad de Viena en 1866. Durante sus estudios universitarios tuvo como profesores a José Petzval, Anrease von Ettinghausen y Joseph Stefan. Entre 1867 y 1869 colaboró con Joseph Stefan en sus investigaciones sobre las pérdidas de energía sufridas por los cuerpos muy calientes.

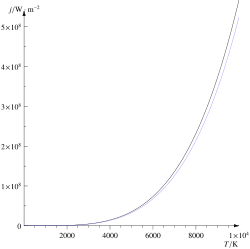
La colaboración entre ambos daría origen a una Ley de gran relevancia en la termodinámica; la Ley de Stefan-Boltzmann. Esta Ley establece que un cuerpo negro emite radiación térmica con una potencia emisiva hemisférica total (W/m²) proporcional a la cuarta potencia de su temperatura.La ley fue deducida en 1879 por el físico austriaco Jožef Stefan (1835-1893) basándose en las mediciones experimentales realizadas por el físico irlandés John Tyndall y fue derivada en 1884 a partir de consideraciones teóricas por Ludwig Boltzmann (1844-1906) usando la termodinámica. tefan publicó esta ley en el artículo «Über die Beziehung zwischen der Wärmestrahlung und der Temperatur» (Sobre la relación entre la radiación y la temperatura térmica) en el Boletín de las sesiones de la Academia de Ciencias de Viena.

Fue profesor de física en Graz entre 1869 y 1873. Luego se trasladó a Heidelberg y a Berlín. En esos lugares estudió con Bunsen, Kirchhoff y Helmholtz. Cuatro años después, en 1873, aceptó un puesto de profesor de matemáticas en Viena. Regresaría, sin embargo, a Graz como catedrático en 1876. En 1894 retomó su puesto, esta vez como profesor de física teórica, en la Universidad de Viena. En 1900, debido a su legendario enfrentamiento con Ernest Mach, Boltzmann se trasladó a Leipzig.

Regersó a la Universidad de Viena en 1902 . En esta ocasión, además de recuperar su cátedra de física, obtuvo la cátedra de Mach de historia y filosofía de las ciencias.

A lo largo de su experiencia como docente, tuvo alumnos como Svante Arrhenius, Walther Nernst de Alemania y Wilhem Ostwald, que pasarían en poco tiempo a formar parte de la Historia de la Ciencia,

Desde 1900 fue miembro de la Academia de Ciencias de Francia y también fue Doctor Honoris Causa por la Universidad de Oxford.

Boltzmann vinculó por primera vez la entropía y la probabilidad en 1877 abriendo el camino a la mecánica estadística. En una serie de trabajos, Boltzmann mostró cómo se podrían aplicar los métodos estadísticos para los gases.

En este sentido, Boltzmann fue el primero en combinar métodos estadísticos con leyes deterministas como las de la mecánica newtoniana (aunque realmente ya en el siglo XVIII Daniel Bernoulli aplicó razonamientos estadísticos para explicar el comportamiento de sistemas de fluidos).

La física estadística o mecánica estadística es una rama de la física que mediante la teoría de la probabilidad es capaz de deducir el comportamiento de los sistemas físicos macroscópicos a partir de ciertas hipótesis sobre los elementos o partículas que los conforman.

A grandes rasgos, la mecánica estadística ignora los comportamientos individuales de las partículas, preocupándose en vez de ello por los promedios.

La estadística de Maxwell-Boltzmann es una función estadística desarrollada para modelar el comportamiento de sistemas físicos regidos por la mecánica clásica. Esta función estadística clásica, formulada originalmente por los físicos J.C. Maxwell y Boltzmann, rige la distribución de un conjunto de partículas en función de los posibles valores de energía de los estados que éstas pueden ocupar.La distribución de Boltzmann o distribución de Maxwell-Boltzmann es una distribución de probabilidad de las velocidades de un gas asociada a la estadística de Maxwell-Boltzmann para dicho sistema.

En honor de Boltzmann se nombró a una de las constantes mas importantes de la termodinámica; la constante de Boltzmann (k o kB) que es la constante física que relaciona temperatura absoluta y energía.

S = k ln W, donde K es la constante de Boltzmann, W el número de formas de ordenación posibles y S la entropía del sistema

Esta ecuación, que relaciona los detalles microscópicos o microestados del sistema (a través de W) con su estado macroscópico (a través de la entropía S), es la idea central de la mecánica estadística.

Como curiosidad, la ecuación aparece grabada en la tumba del propio Botzman.

La relación nunca se expresó a través de una constante específica hasta que Max Planck introdujo por vez primera k, y ofreció un valor exacto (1.346×10−23 J/K, aproximadamente 2.5% menor que la cifra que se usa hoy en día), en su derivación de la ley de la radiación del cuerpo negro en 1900–1901.
Antes de 1900, las ecuaciones que incluían los factores de Boltzmann no utilizaban las energías por molécula ni la constante de Boltzmann, sino una forma de constante de gas R y energías macroscópicas para las cantidades macroscópicas de la sustancia.

Sin embargo las teorías de Boltzmann no tuvieron buena acogida. Muchos de sus artículos fueron rechazados por el editor de una destacada revista de física alemana porque este insistía en que átomos y moléculas eran herramientas convenientes estrictamente teóricas, y no objetos que existieran realmente en la naturaleza. Para muchos de sus coetáneos era difícil aceptar que lo que hasta entonces se consideraban leyes fundamentales de la naturaleza, como el segundo principio de la termodinámica, pudieran tener una interpretación estadística.

Agotado y amargado por tantos ataques personales, Boltzmann se ahorcó en 1906.

Resulta triste pensar que pese a los muchos detractores que tuvieron sus métodos estadísticos, en el año 1900 un joven físico alemán descubrió, gracias en gran parte a las ideas de Boltzmann, la ley de la radiación electromagnética emitida por un cuerpo a una temperatura dada que explicaba el espectro de emisión de un cuerpo negro. Esta ley se convirtió en una de las bases de la mecánica cuántica. Su autor era Max Planck uno de los mas firmes defensores de Boltzmann y que tuvo que recurrir inevitablemente a la mecánica estadística para calcular su famosa constante y su Ley de la radiación. No es arriesgado afirmar que la mecánica cuántica siempre estará en deuda con Boltzmann.

Entre las obras más destacadas de Boltzmann figuran Vorlesungen über die Maxwell’s Theorie der Electricität und des Lichtes (1891), Vorlesungen úber Gaztheorie (dos vols., 1896-98), Escritos populares (1905), Über die Prinzipien der Mechanik (1897) y Wissenschaftliche Abhandlungen (1909).

El «gigante» heliocentrista; Copérnico.

El 19 de febrero de 1473, nacía el astrónomo polaco Nicolás Copérnico (Torun, Prusia, Polonia, 19 de febrero de 1473-Frauenburg, Prusia, Polonia, 24 de mayo de 1543), el fundador de la astronomía moderna. Todo gira en torno al Sol…

Lo que se conoce como Revolución Copernicana es su formulación de la teoría heliocéntrica, según la cual, la Tierra y los otros astros giran alrededor del Sol.

Copérnico realizó su educación básica en Torun y posteriomente en Wloclawek.

Comenzó sus estudios superiores en la Universidad de Cracovia, donde ingresó en 1491 para estudia matemáticas y arte, finalizando los mismos en 1494.

Posteriormente ingresaría, en 1496, en la Universidad italiana de Bolonia para completar su formación donde estudiaría a los humanistas clásicos estudiando, derecho medicina y filosofía. Haría importantes observaciones astronómicas como asistente de su profesor Domenico María de Novara . Abandonaría Bolonia en el año 1499.

En el año 1500 realizaría un curso sobre astronomía y ciencias generales en Roma.

En el año 1501, ingresaría en la Universidad de Padua donde estudiaría Derecho y medicina hasta 1506. En 1503, obtendría su título de Doctor de Derecho Canónico en la Universidad de Ferrara.

En 1506, volvería a Prusia. Entre 1506 y 1512 trabajaría como médico personal de su tio, el obispo de Ermland, fijando su residencia en Heilsberg.

En 1512, se trasladaría a Frauenburg, donde se haría cargo de las obligaciones de canónigo de la Catedral. En Frauenburg, pasaría el resto de su vida interesándose por temas económicos y aplicando sus conocimientos médicos.

En 1509, publicaría su primera obra, la traducción al latín de las cartas de Theophylactus de Simocata escritas originalmente en griego.

Precisamente por sus conocimientos de lenguas clásicas, Copérnico tuvo acceso a la obra del astrónomo greco-egipcio Claudio Ptolomeo (Ptolemaida, Tebaida, c. 100 – Cánope, c. 170).

Copérnico leyó con dedicación su principal obra  el “Almagesto” escrito en el siglo II en  Alejandría,Egipto. Ptolomeo era un continuista del pensamiento aristotélico y en su obra se basaba en el catálogo estelar de  Hiparco de Nicea. Ptolomeo creía que la Tierra estaba inmóvil y ocupaba el centro del Universo, y que el Sol, la Luna, los planetas y las estrellas giraban a su alrededor. Estas ideas las exponía en el primero de los 13 volúmenes de los que consta el Almagesto.

Sin embargo Copérnico dudaba de esas afirmaciones. Tras sus estudios astronómicos en Bolonia y Roma, y su capacidad de observación, el modelo ptolemaico presentaba problemas. No podía explicar, por ejemplo, por qué Venus y mercurio siempre se hallaban en las proximidades del Sol.

Copérnico se comenzó a interesar por la obra del matemático y astrónomo griego Aristarco de Samos ( c. 310 a. C.-c. 230 a. C.), la primera persona que propuso un modelo heliocéntrico del Sistema Solar y que aparecía en citas en las obras de Plutarco y Arquímedes.

Según las ideas de Aristarco, el Sol era el que se encontraba en el centro del Universo conocido. De esta forma el comportamiento de Venus y Mercurio, no sería anómalo sino lógico. Se veían siempre más cerca del Sol, por que realmente estaban más cerca del Sol. La referencia era el Sol y no la Tierra.

En 1516, ordenó sus ideas en su primer tratado astronómico, «De hypothesibus motuum coelestium a se constitutis commentariolus» (popularmente conocido como el «Commentariolus»).

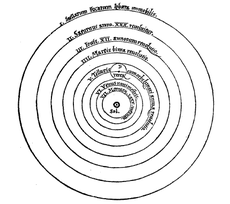En este primer tratado, del que sólo circularon unas pocas copias manuscritas, Copérnico ya exponía la base de sus ideas; el Sol es el centro del universo, la Tierra rota sobre su propio eje y al vez orbita, como el resto de los planetas alrededor del Sol.

La Tierra giraba sobre sí misma una vez al día, y una vez al año daba una vuelta completa alrededor del Sol. El movimiento de los planetas alrededor del Sol describían obras circulares (algo que posteriormente modificaría Kepler en su obra de 1609 “La nueva astronomía”.

Pese a la escasa difusión inicial de su obra, enseguida se extendió por toda Europa. El nombre de Copérnico comenzó a hacerse popular entre los astrónomos y los ambientes científicos en general del viejo continente.

En 1513, Copérnico fue invitado por el obispo Pablo de Middelburg a expresar su opinión en la reforma del calendario juliano en el Concilio de Letrán.

El «Commentariolus» no se publicaría hasta 1878. Copérnico, de personalidad reservada evitaba cualquier posible conflicto con la Iglesia.

Pero «Commentariolus» era sólo un esbozo de lo que sería su obra maestra  “De revolutionibus orbium coelestium”(Sobre las revoluciones de las esferas celestes).

Comenzó a escribirla en 1507, pero no la finalizaría hasta 1532. Y una vez acabada, Copérnico se decidió a no publicarla para evitar cualquier problema. Y ello pese a que, en principio, contaba con el beneplácito de las autoridades eclesiásticas. De hecho en 1533 el Papa Clemente VII ya conocía las ideas de Copérnico por medio de su secretario Johann Albrecht Widmannstetter, e incluso en 1536, el cardenal de Cápua, Nikolaus Cardinal von Schönberg, a instancias de propio Papa llegó a escribir a Copérnico instándole a publicar sus ideas.

No sería hasta 1539, cuando animado por su discípulo  Georg Joachim (más conocido como Rheticus), profesor de matemáticas y astronomía en la Univerisdad de  Wittenberg se decidió a iniciar la publicación.

En 1540 publicaría en Danzing, un pequeño anticipo de la misma “El Narratio prima”,que obtuvo un gran éxito. Finalmente Copérnico fue capaz de hacer frente a sus miedos y dedicarse por completo a la edición del  “De revolutionibus”.

Rheticus le sirvió como asistente y fue el, quién ordenó y copió pacientemente los manuscritos de Copérnico.

Rheticuss, publicó en 1542, a modo de anticipo, un tratado de trigonometría de Copérnico que posteriormente sería incluido en el segundo libro de De revolutionibus.

En 1542, la obra estaba concluida y Copérnico autorizó su publicación a Johannes Petreius en Núremberg. En 1543, por fin, saldrá a la luz uno de los Libros de científicos más importantes de la Historia; “De revolutionibus orbium coelestium”.

El primer ejemplar impreso del libro llegó a manos de Copérnico el 24 de mayo de 1543. Ese mismo día falleció aquejado de una apoplejía en Frauenburg.

“De revolutionibus orbium coelestium”, consta de seis volúmenes.

• El primer volumen contiene una visión general de la teoría heliocéntrica y una corta explicación de sus ideas del universo.
• El segundo volumen es teórico y habla de los principios de la astronomía esférica.
• El tercer volumen habla principalmente de los movimientos del Sol y de los planetas y sus órbitas.
• El cuarto volumen contiene descripciones similares de la Luna y de sus movimientos orbitales.
• El quinto y el sexto volúmenes contienen una explicación del nuevo sistema, el “Systema mundi” Copernicano.

El libro estaba, intencionadamente, dedicado al Papa  Pablo III para evitar cualquier conflicto. Además contaba con un prefacio del filśofo  Andreas Osiander (aunque supuestamente anónimo) en el que se explica que el sistema propuesto constituye una hipótesis matemática para explicar mejor el movimiento de los planetas y otros cuerpos celestes y que no se traducía forzosamente en una realidad.

“De revolutionibus» fue esencial para el posterior desarrollo desarrollo de las astronomía moderna por Tycho Brahe, Johannes Kepler y Galileo.

Tres años después de la publicación de “De revolutionibus· , en 1546, un sacerdote dominico, Giovanni Maria Tolosani, escribe “De veritate Sacrae Scripturae” un escrito donde denuncia las teorías de Copérnico frente a la verdad absoluta de la Biblia

El 5 de marzo de 1616 el Santo Tribunal de la Inquisión hace un análisis de la teoría heliocéntrica expuesta por Nicolás Copérnico. Llega a la conclusión de que esta teoría, aunque no era herética, era contraria a las Escrituras y falsa en la filosofía.

De revolutionibus orbium coelestium» , uno de los libros más importantes de la historia de la ciencia, se convierte en prohibido e ingresa en el en el Index librorum prohibitorum (Índice de libros prohibidos) del que no saldría hasta el año 1835.

Por su enorme contribución a la astronomía, en 1935 se dio el nombre «Copernicus» a uno de los mayores cráteres lunares, ubicado en el Mare Insularum.

En memoria de Nicolás Copérnico, el 19 de febrero de 2010 la IUPAC nombró al elemento 112 de la tabla periódica como copernicio.

El nacimiento de un «gigante»; Galileo.

El 15 de febrero de 1564, nacía uno de los mayores «gigantes» de la Historia de la Ciencia; el astrónomo, filósofo, ingeniero, matemático y físico italiano Galileo Galilei (Pisa, 15 de febrero de 1564 – Arcetri, 8 de enero de 1642).

Ha sido considerado como el “padre de la ciencia moderna” y el primer divulgador científico de la historia. Es, sin duda, una de las figuras clave de la revolución científica del Renacimiento.

Galileo comenzó su formación en su casa de mano de sus padre músico y matemático florentino Vincenzo Galilei. A los diez años ingresó en el convento de Santa María de Vallombrosa. En 1585 comienza sus estudios de matemáticas, medicina y filosofía en la Universidad de Pisa. Accede a las matemáticas de Euclides, que serían fundamentales en su posterior desarrollo científico. En ésta época ya comienza a mostrar su rechazo hacia las posturas aristotélicas hegemónicas en la época, decantándose hacia la experimentación y negando el valor de la metafísica.

Retorna a Florencia en 1585, sin haber obtenido ningún título universitario. Ya por esa época había hecho notables descubrimientos; la ley de la isocronía de los péndulos, el baricentro de los cuerpos, el desarrollo de una balanza hidrostática basada en la desarrollada por Arquímedes con anterioridad o la invención de un primitivo pulsómetro.

En 1589, ingresa como catedrático de matemáticas en la Universidad de Pisa. De esta época datan sus primeros estudios sobre el movimiento, intentando demostrar, tal y como postulaba Arquímedes, que la velocidad de caída de los objetos depende únicamente de su densidad y no de su peso. Pese a la leyenda se cree que es poco probable que dejase caer objetos desde la Torre de Pisa para comprobar sus resultados experimentales (y mos dos balas de cañón como se afirma). Pero sí se sabe que construyo un plan inclinado midiendo la velocidad de descenso de bolas con diferentes densidades y calculando el tiempo de recorrido de éstas mediante un reloj de agua.

En 1592 abandonará su puesto en la Universidad de Pisa, por los paupérrimos ingresos, aceptando el puesto de profesor de geometría, mecánica y astronomía ofrecido por la Universidad de Padua donde permanecería hasta 1610. En 1595, ya en Padua, muestra sus primeras aproximaciones al copernicanismo, al presentar una explicación de las mareas basadas en un ciclo diario y anual del movimiento de la Tierra.

En Padua comenzará asimismo, sus estudios sobre arquitectura militar y topografía entre otras materias. En 1604, el considerado «annus mirabillis» de Galileo descubre la ley del movimiento uniformemente acelerado. En 1606, presenta su primera obra Operaciones del compás geométrico y militar, donde presenta invenciones como una máquina para elevar agua que utilizaba caballos como fuerza motriz , un termoscopio (tratándose del primer aparato de la historia que permitía la comparación objetiva el nivel de calor y de frío, antecesor del moderno termómetro) y un procedimiento mecánico de cálculo.

En 1609, a través de una carta enviada por su antiguo alumno Jacques Badovere, tiene constancia de la existencia de un invento que cambiaría su vida y la Historia. En Holanda, Lipperhey, había construido un aparato que permitía ver objetos a grandes distancias e incluso estrellas invisibles a simple vista. Se trataba del telescopio. Galileo sin tener más información que la proporcionada por Badovere, se decide a construir su propio telescopio. Pero Galileo conseguiría un telescopio perfeccionado; sus aumentos eran de 6 veces (el doble que el original, aunque en posteriores versiones conseguiría alcanzar ya los 9 aumentos), no deforma los objetos y gracias a una lente divergente proporcianaba la imagen al derecho y no invertida, lo que dificultaba mucho la visión.

El 21 de agosto de 1609, la plaza San Marco, Galileo ofrece su invento al Senado de Venecia y lega los derechos a la República de Venecia. Al parecer los miembros del Senado pudieron ver la isla de Murano situada a 2 km y medio. El Senado se entusiasmo con las posibles aplicaciones militares del objeto, por lo que premiaron a Galileo duplicándole su sueldo y ofreciéndole un puesto de trabajo vitalicio en la Universidad de Papua. La suerte de Galileo había cambiado.

El nuevo invento, que iría perfeccionando poco a poco, le otorgó grandes logros en el campo de la astronomía. Aunque el mismo reconocería en marzo de 1610 (y que corroboraría Keppler) que de los aproximadamente 60 telescopios que había construido, muy pocos resultaban adecuados para las labores astronómicas, debido a sus escasos conocimientos en óptica.

El 7 de enero de 1610 Galileo Galilei observa cuatro de las lunas de Júpiter a través de su telescopio; Calixto, Europa, Ganímedes e Ío. Galileo llamará a estos satélites por algún tiempo los “astros mediceos” I, II, III y IV, en honor de Cosme II de Médicis, su antiguo alumno y gran duque de Toscana. Éste le recompensa con el nombramiento de Filósofo y Matemático del Gran Duque.

Galileo consideraba que Júpiter y sus satélites eran una modelización del Sistema Solar, lo que considera un dato fundamental para poder demostrar que las órbitas de cristal de Aristóteles no existen y que todos los cuerpos celestes no giran alrededor de la Tierra. Ponía en cuestión la Teoría geocéntrica adoptada por los ptolomeicos. El 10 de abril, muestra estos astros a la corte de Toscana, siendo todo un éxito. Keppler le ofrece su apoyo sin reservas y Galileo le regala una lente con la que el mismo Keppler podrá corroborar, en septiembre, las teorías de Galileo.

El 4 de marzo de 1610, Galileo publica en Florencia sus descubrimientos dentro de El mensajero de las estrellas (Sidereus nuncius), resultado de sus primeras observaciones estelares. Se trataba del primer tratado científico basado en observaciones astronómicas realizadas con un telescopio. Galielo postulaba que las nebulosas y la propia Vía Láctea estaban formadas por conjuntos de estrellas contrariamente a lo expuesto por Ptolomeo en el Almagesto.

Pero los descubrimientos de Galileo continuarían. De esta forma el 7 de diciembre de 1610, Galileo observa, (ya con un telescopio de 20 aumentos) por primera vez, la superficie irregular de la Luna, descubriendo sus cráteres y montañas.

Galileo denominó «mares» a las manchas oscuras y permanentes que observaba e incluso llegó a medir las alturas de algunos accidentes por la longitud de sus sombras, obteniendo cifras un poco más elevadas que las reales.

En contra de las tesis Aristotélicas, los objetos celestes no son formas perfectas, presentan irregularidades. Otro golpe a las Teorías mayoritarias de la época.

El 11 de diciembre de 1610, comprobó que el planeta Venus tenía fases como la Luna, este dato fue el definitivo para rebatir la tesis geocéntrica ptoloméica.

El 29 de marzo de 1611 es invitado por el cardenal Maffeo Barberini (el futuro Papa Urbano VIII) a presentar sus descubrimientos al Colegio pontifical de Roma . Asimismo realiza su exposición en la primera Sociedad científica moderna La Academia Lincei, fundada en 1603 por Federico Cesi, a la que se verá unido para siempre y que se hará cargo de la publicación del resto de sus obras.

Aunque parecían tiempos gloriosos para Galileo, la tormenta no tardaría en desatarse. Pese a que el 24 de abril de 1611, mismismo Colegio Romano, confirma al cardenal Belarmino que las observaciones de Galileo son exactas sus enemigos se organizan. El propio cardenal Belarmino ordena al Tribunal de la Santa Inquisición la apertura de una investigación sobre Galileo y sus ideas en junio de 1611, apenas dos meses después del informe emitido por el Colegio Romano.

Los años siguientes serán duros para Galileo. Los ataques se sucederán hasta que finalmente el 16 de febrero de 1616 es convocado por el Santo Oficio. La teoría copernicana, defendida por Galileo, es condenada como “una insensatez, un absurdo en filosofía, y formalmente herética”. Resulta un golpe durísimo a las ideas de Galileo. El 25 y 26 de febrero de 1616, la censura es ratificada por la Inquisición y por el papa Paulo V.

El 22 de febrero de 1632, Galileo, publica en Florencia su diálogo de los Massimi sistemi (Diálogo sobre los principales sistemas del mundo). Lo publica además en italiano, en contra del criterio habitual de publicarlo en latín, por lo que se le considera un precursor de la divulgación científica. En el libro, escrito en forma de dialogo entre tres interlocutores, Salviati, Simplicio y Sagrado, se critican duramente los postulados ptoloméicos y aristotélicos comparándolos con los copernicanos.

Tal “osadía” le costaría muy cara a Galileo que tenía prohibido desde 1616 escribir al respecto.

El 12 de abril de 1633, la teoría heliocéntrica propuesta por Galileo Galilei, es declarada herética por la Inquisición romana, el Santo Oficio.

«Y no se puede responder que esto no es materia de fe, porque si no es materia de fe ex parti obiecti (respecto al objeto) es materia de fe ex parte dicentis (por quien lo dice). Y tan herético sería como quien dijera que Abraham no tuvo dos hijos y Jacob doce, o quien dijera que Cristo no nació de Virgen. — Cardenal Belarmino», “Carta a Foscarini”. Opere XII, pp. 171–172.

Y finalmente, tras un juicio irregular el 22 de junio del año 1633, en el convento romano de Santa Maria sopra Minerva, Galileo fue obligado por la Inquisición a negar su herejía: que la Tierra gira alrededor del Sol.

Es la conocida como la abjuración de Galileo Galilei, uno de los episodios más tristes de la Historia de la Ciencia.

Fue obligado a pronunciar de rodillas la abjuración de su doctrina ante la comisión de inquisidores, bajo las órdenes del papa Urbano VIII, que había sido su amigo y que había sentido una profunda admiración por Galileo.

«Yo, Galileo, hijo de Vincenzo Galileo de Florencia, a la edad de 70 años, interrogado personalmente en juicio y postrado antre vosotros, Eminentísimos y Reverendísimos Cardenales, en toda la República Cristiana contra la herética perversidad Inquisidores generales; teniendo ante mi vista los sacrosantos Evangelios, que toco con mi mano, juro que siempre he creído, creo aún y, con la ayuda de Dios, seguiré creyendo todo lo que mantiene, predica y enseña la Santa, Católica y Apostólica Iglesia.

Pero, como, después de haber sido jurídicamente intimado para que abandonase la falsa opinión de que el Sol es el centro del mundo y que no se mueve y que la Tierra no es el centro del mundo y se mueve, y que no podía mantener, defender o enseñar de ninguna forma, ni de viva voz ni por escrito, la mencionada falsa doctrina, y después de que se me comunicó que la tal doctrina es contraria a la Sagrada Escritura, escribí y di a la imprenta un libro en el que trato de la mencionada doctrina perniciosa y aporto razones con mucha eficacia a favor de ella sin aportar ninguna solución, soy juzgado por este Santo Oficio vehementemente sospechoso de herejía, es decir, de haber mantenido y creído que el Sol es el centro del mundo e inmóvil, y que la Tierra no es el centro y se mueve (…)»

Giuseppe Baretti afirmó que después de la abjuración Galileo dijo la famosa frase “Eppur si mueve” (“Y sin embargo se mueve”), no deja de ser un mito, ya que no hay ninguna otra referencia a ésta afirmación.

Desde diciembre de 1633 a 1638, Galileo es obligado a quedar confinado en su residencia, bajo arresto domiciliario. Pese a lo cruel de la sentencia,  había tenido «suerte. Su inquisidor, el cardenal Bellarmino, se había hecho cargo en 1598 asimismo del proceso inquisitorial contra Giordano Bruno, llevando a éste a morir quemado en la hoguera.

Pese a ello su obra se extenderá por Europa en su forma latinizada, especialmente en Francia. Finalmente en 1638, será publicada en Leiden, por Louis Elsevier su «Discursos sobre dos nuevas ciencias» su última obra.

El 8 de enero de 1642, Galileo, que ya se había quedado ciego en 1638, muere en Arcetri a la edad de 77 años.

En Indiana, por Ley, π vale…3,2.

El 5 de febrero 1897, en el estado estadounidense de Indiana, se propuso por Ley otorgar un valor fijo y único a pi: 3,2. El proyecto de ley de Indiana sobre π (Pi) (en inglés Indiana Pi Bill).

En la Asamblea General de Indiana, se tramitó el proyecto de Ley No.246. “Un proyecto de ley que presenta una nueva verdad matemática y que es ofrecido como una contribución a la educación que solo podrá ser utilizado por el Estado de Indiana en forma gratuita sin necesidad de pagar ningún tipo de royalties, siempre y cuando sea aceptado y adoptado en forma oficial por la legislatura en 1897”.

Se convertiría en una de las propuestas más absurdas de legislar sobre la Ciencia en la Historia.

La propuesta fue planteada por el representante de la Asamblea General Taylor en nombre de un aficionado a las matemáticas, el Dr. Edwin J. Goodwin, un médico del Estado, que había planteado lo siguiente:

«La relación entre el diámetro y la circunferencia [PI] es de cinco cuartas partes a cuatro. Es decir (4 dividido por 5/4 = 16/5 = 3,2 exactamente”.

El proyecto fue aprobado por la Asamblea General de Indiana por unanimidad (67 votos favorables y ninguno contrario…).

Por fortuna, cuando el Proyecto de Ley se estaba tramitando en el Senado (después de obtener el informe favorable del Comité de Educación…) un profesor de la Universidad Perdue de Lafayette, el matemático Clarence A. Waldo Clarence Abiathar Waldo (January 21, 1852 – October 1, 1926), demostró la incoherencia matemática de tal aseveración.

Waldo debió ser muy persuasivo ya que el Proyecto de Ley fue pospuesto el 12 de febrero de 1897 de forma indefinida.

Realmente el caso tenía una trasfondo económico encubierto.

El American Mathematical Monthly había publicado un artículo de Edwin J. Goodwin con el título “Cuadratura del círculo”. Tras una serie de tediosas y absurdas operaciones matemáticas, obtenía un valor para pi de 3,2.

En 1882, el matemático alemán Ferdinand von Lindemann (Hannover, 12 de abril de 1852 – Múnich, 6 de marzo de 1939) ya había demostrado con rigurosidad la imposibilidad de cuadrar el círculo utilizando solo un compás y una regla y que que el número π es un número trascendental,pero poco pareció importarle a Goodwin.

Edwin J. Goodwin, se había apresurado a patentar su “descubrimiento” en los Estados Unidos y varios países europeos. Es decir, acababa de privatizar el conocimiento científico universal, así sin más…

Como dijo un representante del Senado “ Si aprobamos esta ley, que fija un nuevo valor correcto del número pi, el autor nos ofrece la posibilidad de utilizar su descubrimiento sin coste alguno y publicarlo en nuestros libros de texto, mientras que todos los demás usuarios tendrán que pagarle un canon por el uso” . Un negocio redondo, perdón…circular.

Ahora bien, las consecuencias educativas serían obviamente terribles, pero ¿y las económicas?. Ningún objeto circular fabricado en Indiana sería compatible en otro lugar del mundo, desde una rueda, hasta la lente de un telescopio. Una barbaridad absoluta.

Dejándonos de tonterías (con perdón), lo cierto es que pi es una constante matemática muy atractiva (tal vez la más atractiva junto con e) para el público en general.

π (pi) es la relación entre la longitud de una circunferencia y su diámetro, en geometría euclidiana. Pi (π) tiene un valor aproximado de 3,14159265358979… Desde tiempos inmemoriales se ha tratado de obtener su valor exacto. En el papiro Rhind del escriba egipcio Ahmes en el año1800 a. C., ya aparece un intento de obtener su valor. Hoy en día sólo sabemos que cuenta con billones de dígitos que siguen aumentando.

La notación con la letra griega π proviene de la inicial de las palabras de origen griego περιφέρεια ‘periferia’ y περίμετρον ‘perímetro’ de un círculo- El rpiemro en emplear esta notación nor William Oughtred (1574-1660) aunque realmente su uso fue popularizado por el ”gigante” matemático Leonhard Euler (Basilea, Suiza, 15 de abril de1707 – San Petersburgo, Rusia, 18 de septiembre de 1783), en su obra de 1748 “Introductio in analysin infinitorum“ (Introducción al cálculo infinitesimal).

El 14 de marzo, anualmente, se conmemora el día de π. Se realiza ese día por el formato usado en los Estados Unidos, para escribir el 14 de marzo (3/14)

Fue una propuesta del físico Larry Shaw para popularizar la ciencia y que se ha hecho mundialmente famosa con numerosos actos.

En 2009 una resolución favorable de la Cámara de Representantes de los Estados Unidos, declaraba al 14 de marzo como día nacional de π.

El «gigante»con conciencia; Bertrand Russell.

El 2 de febrero de 1970, fallecía una de las mentes más brillantes del siglo XX, el filósofo, matemático, lógico, activista social y escritor británico, ganador del Premio Nobel de Literatura Bertrand Arthur William Russell (Trellech, 18 de mayo de 1872 – Penrhyndeudraeth, 2 de febrero de 1970).

En 1890, Russell ingresó al Trinity College de Cambridge para estudiar matemáticas. Durante su cuarto año en Cambridge, en 1894, Russell estudió Ciencias Morales (Filosofía). En 1895 obtuvo una beca en la Universidad de Cambridge.

En el año 1900 participa en el Congreso Matemático de París, donde quedaría seducido por las aportaciones del matemático, lógico y filósofo italiano Giuseppe Peano (Spinetta, 27 de agosto de 1858 – Turín, 20 de abril de 1932). La obra de Peano sería fundamental en el desarrollo de sus ideas.
Russell, publicaría en 1897, “An essay on the foundations of geometry “ (Ensayo sobre los fundamentos de la geometría).

En 1903 escribe “Los principios de la matemática” y en colaboración con Alfred Whitehead comienza a desarrollar la lógica matemática de Peano y Gottlob Frege. La colaboración con Whitehead culminaría con la publicación de los tres volúmenes de la obra Principia mathematica donde defendía una interpretación de la matemática en términos de la lógica. Asimismo exponía la «teoría de los tipos», la de los números como «clases de clases» y la «paradoja de Russell». A Russell se le considera el fundador de la filosofía analítica.

En esos años comenzaría su activismo político. Después de la primera Guerra Mundial recibió una multa de 100 libras por escribir un folleto donde criticaba con dureza una sentencia de dos años de prisión a la que se había condenado un objetor de conciencia.

Precisamente por su activismo político, la Universidad de Cambridge le retiró su cátedra en 1916. No la recuperaría hasta 1944.

La Universidad de Havard le ofreció un puesto como profesor, pero el Gobierno británico le negó el necesario pasaporte para trasladarse a los Estados Unidos.

En 1918 fue sentenciado a seis meses de prisión por un artículo pacifista que había escrito en The Tribunal.

Durante su estancia en la cárcel, en 1919 escribiría Introduction to Mathematical Philosophy (Introducción a la Filosofía Matemática).

En 1921, recopilaría una serie de conferencias realizadas en Londres en su obra Analysis of Mind (Análisis de la mente).

En 1920, realizaría visitas a la Unión Soviética y a China donde impartiría una serie de conferencias.

En 1924 publicaría «Los caminos de la libertad» (1924) en la Russell abordaba la historia del socialismo, el anarquismo y el sindicalismo.

En 1927 publica Analysis of Matter (Análisis de la materia).

Russell entre 1927 y 1932, dirigiría una escuela infantil en Beacon Hill, Londres interesado en la puesta en práctica de los nuevos métodos pedagógicos.

Durante esa época publicaría buena parte de sus obras sobre la moral y el comportamiento humano; Marriage and Morale, 1929 (Matrimonio y moral), The Conquest of Happiness, 1930 (La conquista de la felicidad ) o Education and the Social Order, 1932 (La educación y el orden social).

Desde 1938 y hasta 1940 colaboraría con diversas Universidades estadounidenses, En 1938 sería nombrado profesor visitante de Filosofía en la Universidad de Chicago. En 1939 sería profesor en Universidad de California. Posteriormente sería invitado a dar clase de matemáticas en la Universidad de Nueva York. Sin embargo, debido a las fuertes presiones en las que se cuestionaban sus opiniones sobre la vida sexual, tuvo que renunciar a la misma.

Se le reprochó el haber escrito en 1929 «Vieja y nueva moral sexual» donde analizaba el comportamiento sexual de la sociedad y hablaba de tabúes para la época como el divorcio o la prostitución.

En 1945 publicaría uno de sus libros fundamentales «Historia de la filosofía occidental», en el que analiza con detalle el desarrollo del pensamiento filosófico.

Respecto a la Ciencia, Russell era un un ferviente defensor del empirismo científico y así lo expuso en 1914 su libro , Our knowledge of the external world as a field for scientific method in philosophy (Nuestro conocimiento del mundo exterior). Russell tuvo una influencia decisiva sobre filósofos de la Ciencia como Karl Popper.
Russell escribiría varios libros de Ciencia como The ABC of atoms (El ABC de los átomos), en 1923, y The ABC of relativity (El ABC de la relatividad), en 1925.

Durante la Segunda Guerra Mundial Russell expresó sus temores sobre el fascismo. Pero el acontecimiento que le marcaría profundamente del conflicto sería la detonación de las dos bombas atómicas en Hiroshima y Nagasaki. Horrorizado de las consecuencias se convertiría en un ferviente activista antinuclear.

En 1950 recibió el Premio Nobel de Literatura «en reconocimiento de sus variados y significativos escritos en los que defiende ideales humanitarios y la libertad de pensamiento».

El 9 de julio de 1955 en Londres, el filósofo y matemático Bertrand Russell presenta el Manifiesto Russell-Einstein sobre la necesidad de un desarme nuclear.

Los firmantes eran científicos de todo el mundo, de enorme reputación que se oponían al uso de las armas nucleares como armas de guerra y advertían de sus consecuencias. Los firmantes fueron: Max Born, Percy W. Bridgman, Albert Einstein, Leopold Infeld, Jean Frédéric Joliot-Curie, Herman J. Muller, Linus Pauling, Cecil F. Powell, Józef Rotblat, Bertrand Russell y Hideki Yukawa.

Se convirtió en un hecho histórico.

El manifiesto se reveló en una conferencia de prensa en el Caxton Hall, Londres, presidida por Rotblat. Russell comenzó la conferencia diciendo:

«Traigo la advertencia pronunciada por los signatarios a la atención de todos los gobiernos de gran alcance del mundo en la esperanza seria que pueden acordar permitir que sobrevivan sus ciudadanos.»

Tras su muerte, el Trinity College de Cambridge descubrió una placa conmemorativa en su honor que supone un excelente resumen de su vida y obra.

«El tercer conde Russell, O.M., profesor de este colegio, fue particularmente famoso como escritor intérprete de la lógica matemática. Abrumado por la amargura humana, en edad avanzada, pero con el entusiasmo de un joven, se dedicó enteramente a la preservación de la paz entre las naciones, hasta que finalmente, distinguido con numerosos honores y con el respeto de todo el mundo, encontró descanso a sus esfuerzos en 1970, a los 97 años de edad.»